Emmanuel Trizac, Marie Chupeau (LPTMS), Alexei Chepelianskii (LPS)
Arrhenius’ law (1889) is a cornerstone in our understanding of many kinetic processes in chemistry, thermodynamics or molecular biology. This empirical law stipulates that reaction rates depend exponentially on the energy barrier which separates the reactants from the final products; this is the so-called activation energy. A satisfactory theory was proposed 50 years later by Kramers for Brownian systems. Kramers’ relationship introduces the coupling to the environment (the suspending fluid) via a friction parameter, and confirms the exponential relationship between reaction speed and activation energy. It is therefore natural to think that the higher the activation barrier, the slower it is to cross, and therefore to conclude that the absence of the activation barrier would lead to maximum reaction rates. A collaboration between the LPS Orsay and the LPTMS, as well as the Cavendish laboratory in Cambridge has shown that this intuition based on the relationships of Kramers / Arrhenius was incorrect. In other words, it is not the free diffusion and therefore without any barrier which minimizes the time of first passage at a target point for a Brownian particle. The very existence of a barrier speeds up the process!
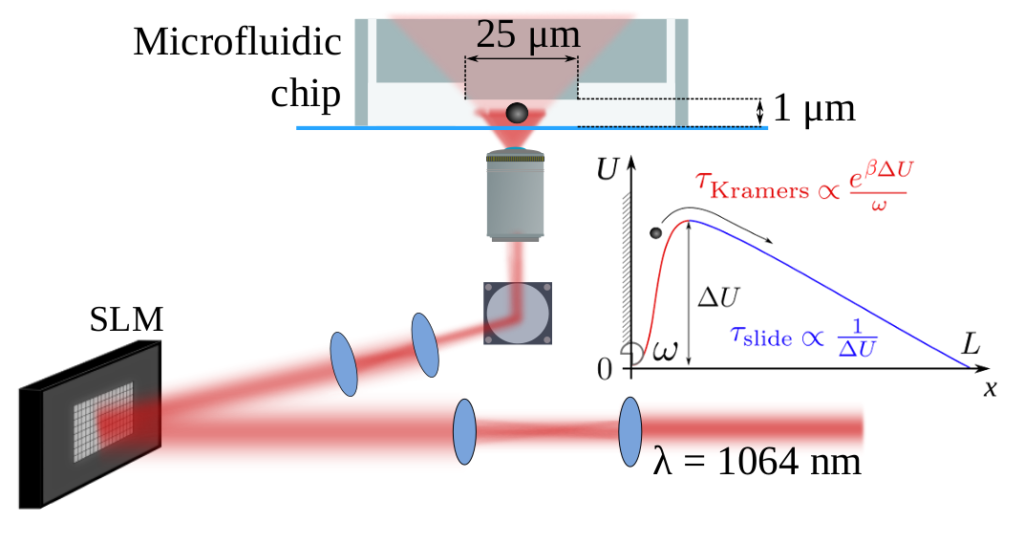
This figure shows the experimental setup to measure the escape rates of a Brownian colloidal particles in an external potential defined with holographic optical tweezers. It also shows the sketch of a theoretical potential profile where the increase of the Kramers escape time is compensated by a fast sliding time. The potential energy at the initial and escape points is equal, a general strategy is proposed to generate optimized ‘accelerating’ potentials with escape rates much faster than free diffusion.
Marie Chupeau, Jannes Gladrow, Alexei Chepelianskii, Ulrich F. Keyser, Emmanuel Trizac, Optimizing Brownian escape rates by potential shaping, Proceedings of the National Academy of Sciences, 201910677 (2019) DOI:10.1073/pnas.1910677116
Résultats obtenus dans le cadre du projet SWEET financépar le thème 2 du LabEx PALM et portépar Emmanuel Trizac (LPTMS) et Alexei Chepelianski (LPS)