Emmanuel Trizac, Marie Chupeau (LPTMS), Alexei Chepelianskii (LPS)
La loi d’Arrhénius (1889) est la pierre angulaire de la compréhension de nombreux processus cinétiques en chimie, en thermodynamique ou en biologie moléculaire. Cette loi empirique stipule que les vitesses de réaction dépendent exponentiellement de la barrière d’énergie qui sépare les réactifs des produits finaux ; on parle d’énergie d’activation. Une théorie satisfaisante en a été proposée 50 ans plus tard par Kramers pour les systèmes browniens. La relation de Kramers introduit le couplage à l’environnement (le fluide porteur) via un paramètre de friction, et confirme la relation exponentielle entre vitesse de réaction et énergie d’activation. Il est ainsi naturel de penser que plus la barrière d’activation est élevée et plus son franchissement est ralenti, et par conséquent de conclure que l’absence de barrière d’activation conduirait aux vitesses de réaction maximales. Une collaboration entre le LPS Orsay et le LPTMS (depuis peu voisins sur le plateau de Saclay), ainsi que le laboratoire Cavendish à Cambridge a montré que cette intuition fondée sur les relations de Kramers/Arrhénius était incorrecte. En d’autres termes, ce n’est pas la diffusion libre et donc sans aucune barrière qui minimise le temps de premier passage à un point cible pour une particule brownienne. L’existence même d’une barrière permet d’accélérer le processus !
Dans ce travail, les physiciens se sont intéressés au temps de premier passage en un point cible pour un objet brownien au voisinage d’une paroi, par exemple une macromolécule micrométrique dans un fluide porteur comme l’eau. Il ont cherché quel profil d’activation maximise la vitesse de réaction ; on peut visualiser une barrière d’énergie dont l’amplitude dépend de la position. Entre le point de départ de la particule et le point cible, l’énergie doit être la même pour ne pas introduire de biais dans le mouvement. En fonction des contraintes expérimentales comme la limitation d’amplitude des barrières d’activation que l’on peut créer in situ, les chercheurs ont calculé les barrières optimales, et montré qu’elles présentent de manière générique un profil spatial « en N ». Forts de ces prédictions théoriques, ils ont recréé les profils optimaux dans des expériences de microfluidique où des pinces optiques holographiques permettent d’imprimer un profil de barrière choisi sur le trajet de la particule, une bille de polystryrène sphérique de 350 nm dans l’eau. Alors même que la barrière en question représente un obstacle sur le trajet de la bille, les physiciens ont mesuré une accélération d’un facteur deux par rapport au cas de référence sans aucune barrière : en moyenne le point cible est atteint deux fois plus vite. En théorie, l’accélération pourrait être supérieure de plusieurs ordres de grandeur… en augmentant la hauteur de la barrière expérimentale, et en confinant la bille d’autant plus étroitement que la barrière est haute ! Ce travail éclaire d’un jour nouveau le phénomène d’activation thermique, essentiel dans les questions de stockage magnétique de l’information, de dynamique chimique, de diffusion atomique ou de repliement des protéines. Suivant que l’on cherche à favoriser ou à inhiber l’activation thermique, des profils de barrière spécifiques doivent être choisis, et mis en œuvre expérimentalement.
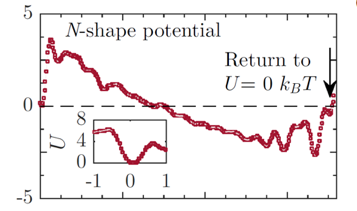
Profil de potentiel « en N » utilisé dans les expériences. La particule brownienne part de x=0 (à gauche), et on étudie son temps de premier passage au point cible indiqué par la flèche, à droite. Entre les points de départ et d’arrivée, la différence d’énergie est nulle. Le fait d’avoir à franchir une barrière d’énergie (représentée en rouge) accélère le transport, par rapport au cas de la diffusion libre (ligne pointillée horizontale correspondant à l’absence de barrière).
Marie Chupeau, Jannes Gladrow, Alexei Chepelianskii, Ulrich F. Keyser, Emmanuel Trizac, Optimizing Brownian escape rates by potential shaping, Proceedings of the National Academy of Sciences, 201910677 (2019) DOI:10.1073/pnas.1910677116
Résultats obtenus dans le cadre du projet SWEET financépar le thème 2 du LabEx PALM et portépar Emmanuel Trizac (LPTMS) et Alexei Chepelianski (LPS)